用 Tensorflow 可视化梯度下降
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
LR=.1
REAL_PARAMS=[1.2,2.5]
INIT_PARAMS=[[5,4],
[5,1],
[2,4.5]][2]
x=np.linspace(-1,1,200,dtype=np.float32)
y_fun = lambda a, b: a * x + b
tf_y_fun = lambda a, b: a * x + b
noise=np.random.randn(200)/10
y=y_fun(*REAL_PARAMS)+noise
a,b=[tf.Variable(initial_value=p,dtype=tf.float32) for p in INIT_PARAMS]
pred=tf_y_fun(a,b)
mse=tf.reduce_mean(tf.square(y-pred))
train_op=tf.train.GradientDescentOptimizer(LR).minimize(mse)
a_list,b_list,cost_list=[],[],[]
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(400):
a_,b_,mse_=sess.run([a,b,mse])
a_list.append(a_)
b_list.append(b_)
cost_list.append(mse_)
result,_=sess.run([pred,train_op])
print('a=',a_,'b=',b_)
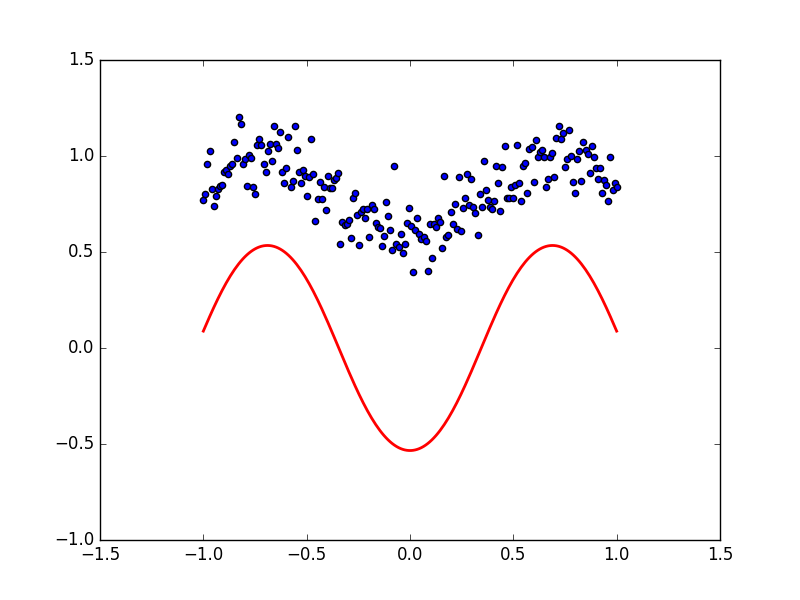
plt.figure(1)
plt.scatter(x,y)
plt.plot(x,result,color='r',linewidth=5)
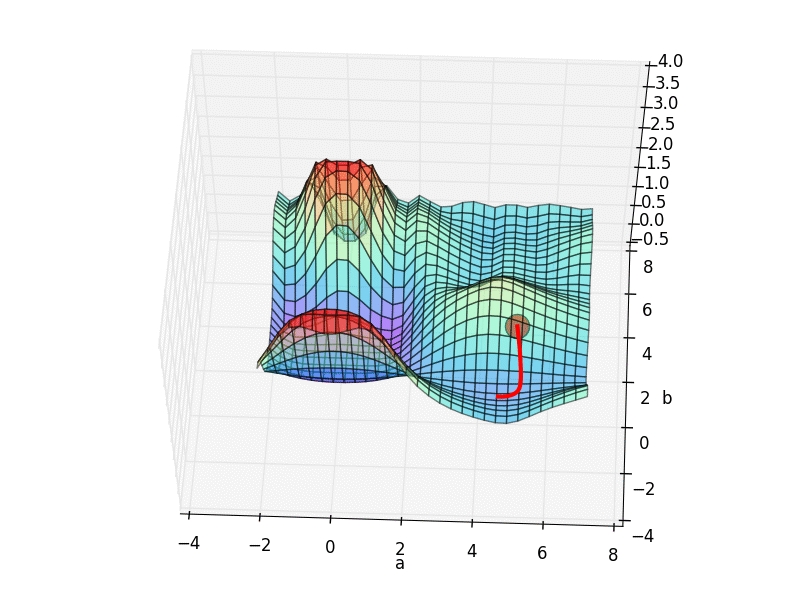
fig=plt.figure(2)
ax=Axes3D(fig)
a3D,b3D=np.meshgrid(np.linspace(-2,7,30),np.linspace(-2,7,30))
cost3D=np.array([np.mean(np.square(y_fun(a_,b_)-y))for a_,b_ in zip(a3D.flatten(),b3D.flatten())]).reshape(a3D.shape)
cost3D_min=cost3D.min()
c3_argmin=cost3D.argmin()
m,n=divmodc3_argmin,30)
a3_perfect=a3D[m][n]
b3_perfect=b3D[m][n]
ax.plot_surface(a3D,b3D,cost3D,rstride=1,cstride=1,cmap=plt.get_cmap('rainbow'),alpha=.85)
ax.scatter(a_list[0],b_list[0],zs=cost_list[0],s=300,c='r')
ax.scatter(a3_perfect,b3_perfect,c3D_min,s=100,c='green')
ax.set_xlabel('a')
ax.set_xlim((-2,7))
ax.set_ylabel('b')
ax.set_ylim((-2,7))
ax.plot(a_list,b_list,zs=cost_list,zdir='z',c='r',lw=3)
plt.show()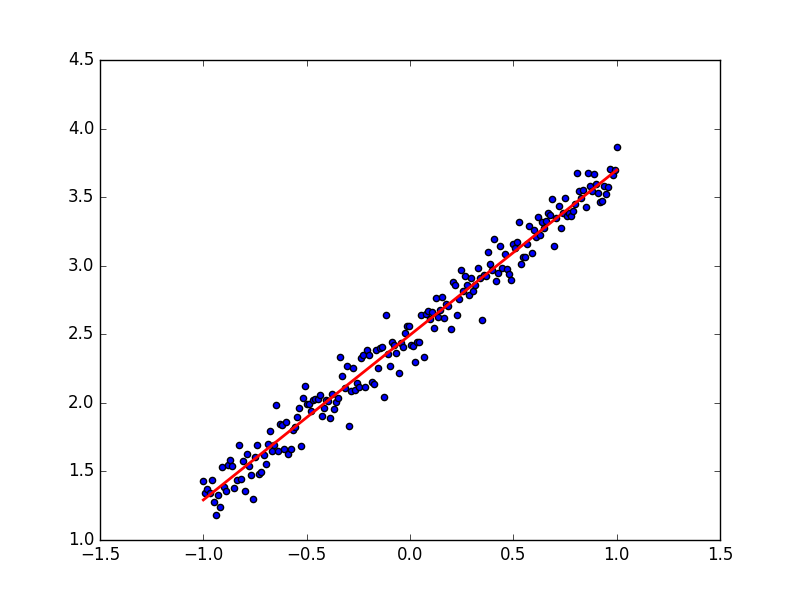
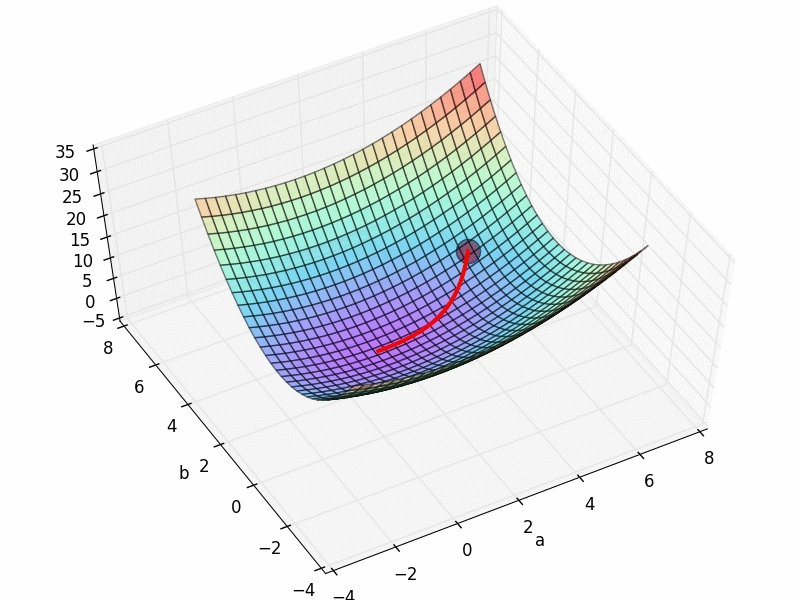
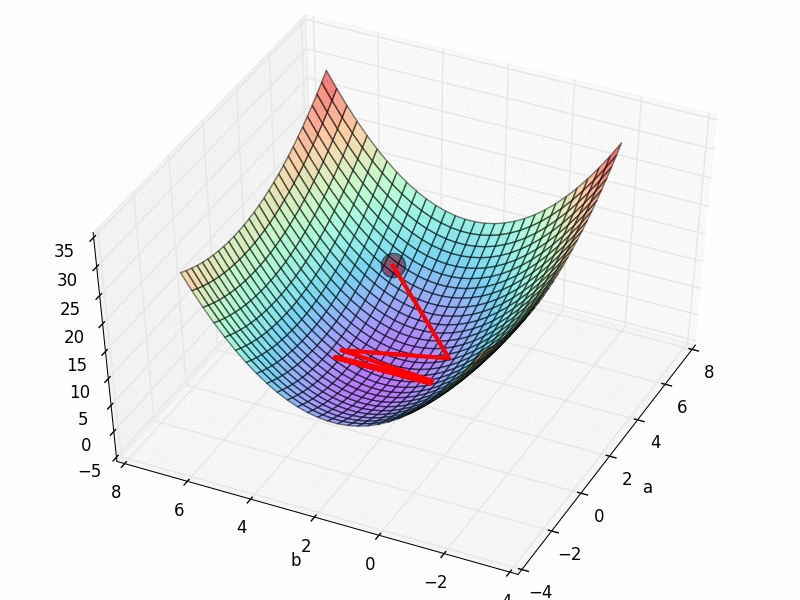
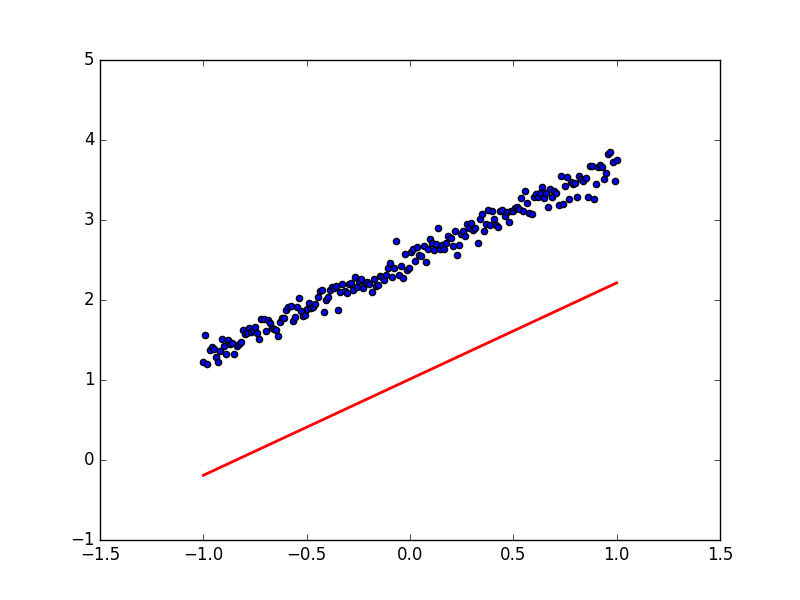
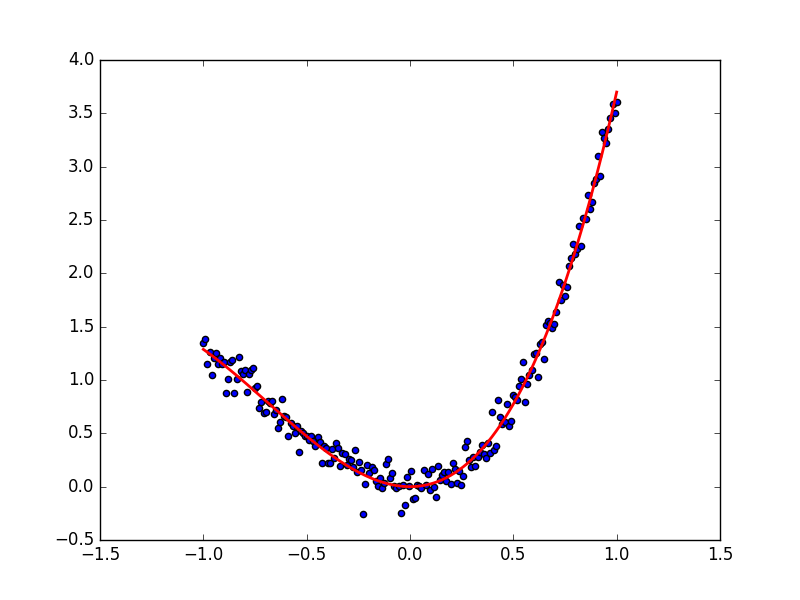
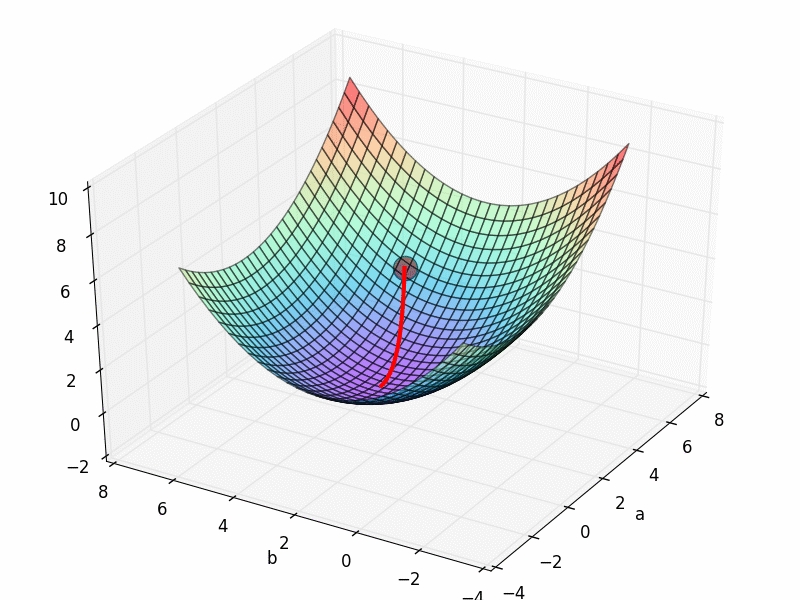
局部最优,全局最优
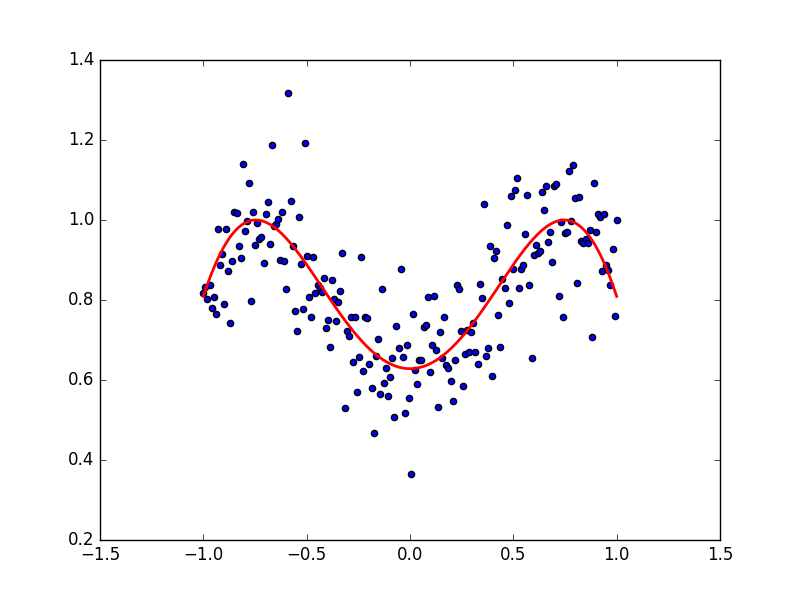
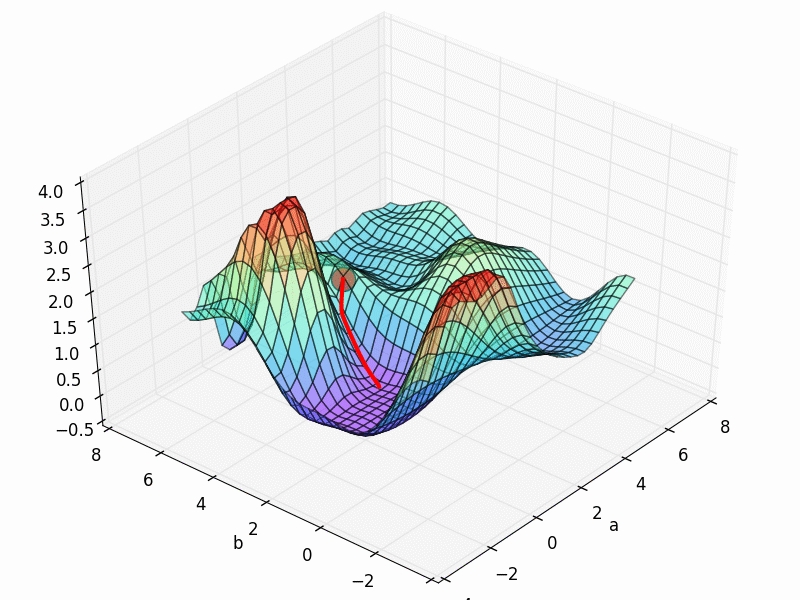
Last updated