1.10 长短期记忆（LSTM（long short term memory）unit）

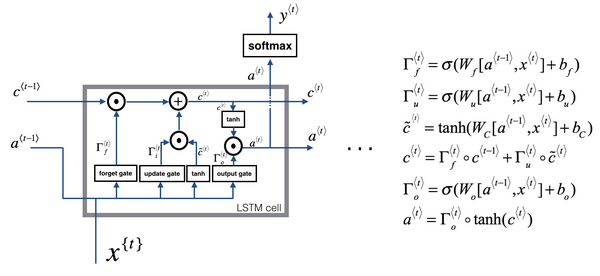
LSTM是另一种更强大的解决梯度消失问题的方法。它对应的RNN隐藏层单元结构如下图所示：

相应的表达式为：

$$\tilde c^{<t>}=tanh(W_c[a^{<t-1>},x^{<t>}]+b_c)$$

$$\Gamma_u=\sigma(W_u[a^{<t-1>},x^{<t>}]+b_u)$$

$$\Gamma_f=\sigma(W_f[a^{<t-1>},x^{<t>}]+b_f)$$

$$\Gamma_o=\sigma(W_o[a^{<t-1>},x^{<t>}]+b_o)$$

$$c^{<t>}=\Gamma_u*\tilde c^{<t>}+\Gamma_f*c^{<t-1>}$$

$$a^{<t>}=\Gamma_o*c^{<t>}$$

LSTM包含三个gates：$\Gamma_u,\Gamma_f,\Gamma_o$，分别对应update gate，forget gate和output gate

在LSTM中不再有$a^{<t>} = c^{<t>}$的情况

红线显示了只要正确地设置了遗忘门和更新门，LSTM很容易把$c^{<0>}$的值一直往下传递到右边，比如$c^{<3>} = c^{<0>}$。这就是为什么LSTM和GRU非常擅长于长时间记忆某个值

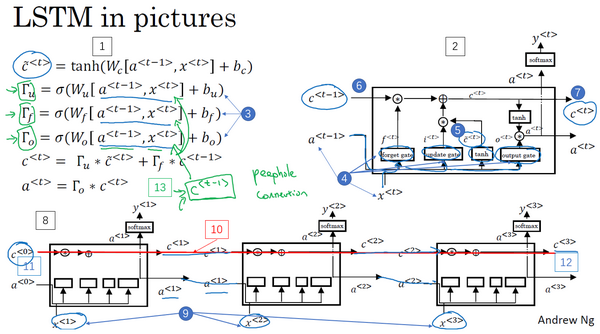
“窥视孔连接”（peephole connection）:门值不仅取决于$a^{<t-1>}$和$x^{<t>}$，也取决于上一个记忆细胞的值（$c^{<t-1>}$），即$c^{<t-1>}$也能影响门值

如果考虑$c^{<t-1>}$对$\Gamma_u,\Gamma_f,\Gamma_o$的影响，可加入“窥视孔连接”，对LSTM的表达式进行修改：

$$\tilde c^{<t>}=tanh(W_c[a^{<t-1>},x^{<t>}]+b_c)$$

$$\Gamma_u=\sigma(W_u[a^{<t-1>},x^{<t>},c^{<t-1>}]+b_u)$$

$$\Gamma_f=\sigma(W_f[a^{<t-1>},x^{<t>},c^{<t-1>}]+b_f)$$

$$\Gamma_o=\sigma(W_o[a^{<t-1>},x^{<t>},c^{<t-1>}]+b_o)$$

$$c^{<t>}=\Gamma_u*\tilde c^{<t>}+\Gamma_f*c^{<t-1>}$$

$$a^{<t>}=\Gamma_o*c^{<t>}$$

LSTM主要的区别：比如（上图编号13）有一个100维的隐藏记忆细胞单元，第$i$个$c^{<t-1>}$的元素只会影响第$i$个元素对应的那个门，所以关系是一对一的，并不是任意这100维的$c^{<t-1>}$可以影响所有的门元素

LSTM前向传播图：

GRU：模型简单，更容易创建一个更大的网络，只有两个门，在计算上运行得更快，且可以扩大模型的规模

LSTM：更加强大和灵活，因为它有三个门而不是两个