1.9 GRU单元（Gated Recurrent Unit（GRU））

门控循环单元：改变了RNN的隐藏层，使其可以更好地捕捉深层连接，并改善了梯度消失问题

简化的GRU模型

RNN隐藏层的单元的可视化：

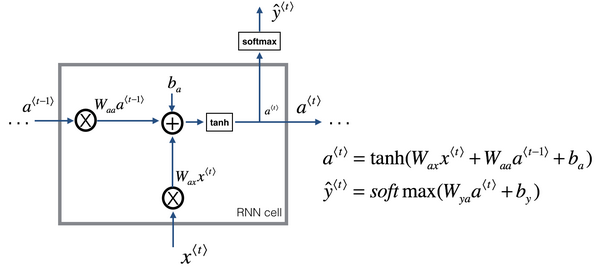
$a^{<t>}$表达式为：

$$a^{<t>}=tanh(W_a[a^{<t-1>},x^{<t>}]+b_a)$$

为了解决梯度消失问题，对上述单元进行修改，添加了记忆单元，构建GRU，如下图所示：

表达式为：

$$\tilde c^{<t>}=tanh(W_c[c^{<t-1>},x^{<t>}]+b_c)$$

$$\Gamma_u=\sigma(W_u[c^{<t-1>},x^{<t>}]+b_u)$$

$$c^{<t>}=\Gamma_u*\tilde c^{<t>}+(1-\Gamma_u)*c^{<t-1>}$$

$c^{<t-1>}=a^{<t-1>}$，$c^{<t>}=a^{<t>}$。符号$c$表示记忆细胞的值，$a$表示输出的激活值，$\tilde c^{<t>}$是个候选值，替代了c的值，$\Gamma_u$（0到1）意为gate，u表示“update”，当$\Gamma_u=1$时，代表更新；当$\Gamma_u=0$时，代表记忆，保留之前的模块输出。$\Gamma_u$能够保证RNN模型中跨度很大的依赖关系不受影响，消除梯度消失问题

完整的GRU

完整的GRU添加了另外一个gate，即$\Gamma_r$，表达式如下：

$$\tilde c^{<t>}=tanh(W_c[\Gamma_r*c^{<t-1>},x^{<t>}]+b_c)$$

$$\Gamma_u=\sigma(W_u[c^{<t-1>},x^{<t>}]+b_u)$$

$$\Gamma_r=\sigma(W_r[c^{<t-1>},x^{<t>}]+b_r)$$

$$c^{<t>}=\Gamma_u*\tilde c^{<t>}+(1-\Gamma_u)*c^{<t-1>}$$

$$a^{<t>}=c^{<t>}$$

$\Gamma_{r}$门：计算出的下一个$c^{<t>}$的候选值${\tilde{c}}^{<t>}$跟$c^{<t-1>}$有多大的相关性

$c^{<t>}$可以是一个向量（编号1），如果有100维的隐藏的激活值，那么$c^{<t>}$、${\tilde{c}}^{<t>}$、$\Gamma_{u}$还有画在框中的其他值也是100维

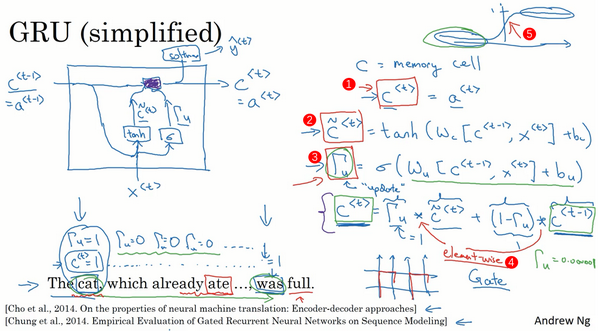
$*$实际上就是元素对应的乘积（$c^{<t>}=\Gamma_u*\tilde c^{<t>}+(1-\Gamma_u)*c^{<t-1>}$），若$\Gamma_{u}$（$\Gamma_u=\sigma(W_u[c^{<t-1>},x^{<t>}]+b_u)$）是一个100维的向量，而里面的值几乎都是0或者1，则这100维的记忆细胞$c^{<t>}$（$c^{<t>}=a^{<t>}$，编号1）就是要更新的比特