1.2 偏差，方差（Bias /Variance）

在一个只有$x_1$和$x_2$两个特征的二维数据集中，可以绘制数据，将偏差和方差可视化。

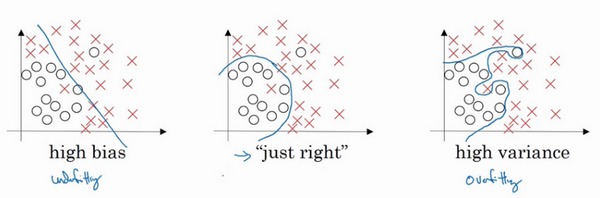
在多维空间数据中，绘制数据和可视化分割边界无法实现，但可以通过几个指标，来研究偏差和方差

理解偏差和方差的两个关键数据是训练集误差（Train set error）和验证集误差（Dev set error）

假定训练集误差是1%，验证集误差是11%，可以看出训练集设置得非常好，而验证集设置相对较差，可能过度拟合了训练集，验证集并没有充分利用交叉验证集的作用，这种情况称之为“高方差”。

假设训练集误差是15%，验证集误差是16%，该案例中人的错误率几乎为0%，算法并没有在训练集中得到很好训练，如果训练数据的拟合度不高，就是数据欠拟合，这种算法偏差比较高。对于验证集产生的结果却是合理的，验证集中的错误率只比训练集的多了1%，这种算法偏差高，因为它甚至不能拟合训练集

训练集误差是15%，偏差相当高，验证集的评估结果更糟糕，错误率达到30%，这种算法偏差高，因为它在训练集上结果不理想，而且方差也很高，这是方差偏差都很糟糕的情况

训练集误差是0.5%，验证集误差是1%，猫咪分类器只有1%的错误率，偏差和方差都很低

以上分析都是基于假设预测的，训练集和验证集数据来自相同分布，假设人眼辨别的错误率接近0%，一般来说，最优误差也被称为贝叶斯误差，最优误差接近0%，如果最优误差或贝叶斯误差非常高，比如15%。再看看这个分类器（训练误差15%，验证误差16%），15%的错误率对训练集来说也是非常合理的，偏差不高，方差也非常低

偏差和方差都高：

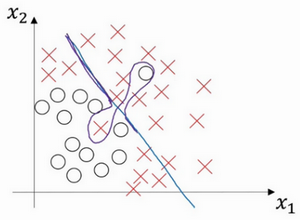
这条曲线中间部分灵活性非常高，却过度拟合了这两个样本，这类分类器偏差很高，因为它几乎是线性的

采用曲线函数或二次元函数会产生高方差，因为曲线灵活性太高以致拟合了这两个错误样本和中间这些活跃数据。但对于高维数据，有些数据区域偏差高，有些数据区域方差高，所以在高维数据中采用这种分类器看起来就不会那么牵强