2.3 词嵌入的特性（Properties of Word Embeddings）

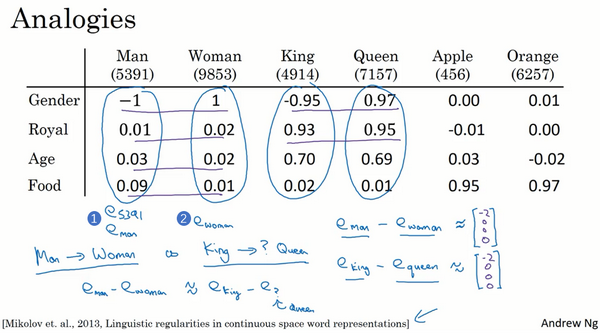
该例中，假设用的是四维的嵌入向量，假如向量$e_{\text{man}}$和$e_{\text{woman}}$、$e_{\text{king}}$和$e_{\text{queen}}$ 分别进行减法运算，相减结果表明，“Man”与“Woman”的主要区别是性别，“King”与“Queen”也是一样

所以当算法被问及man对woman相当于king对什么时，算法所做的就是计算$e_{\text{man}}-e_{\text{woman}}$，然后找出一个向量也就是找出一个词，使得：

$$e_{\text{man}}-e_{\text{woman}}\approx e_{\text{king}} - e_{?}$$

即当这个新词是queen时，式子的左边会近似地等于右边

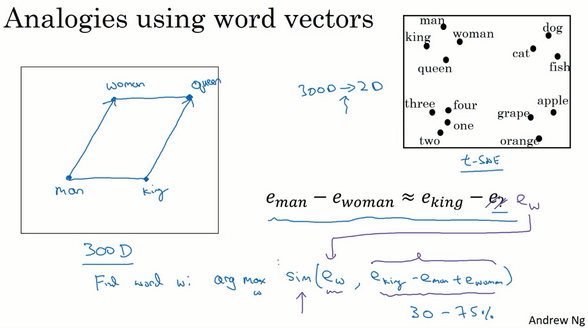
在图中，词嵌入向量在一个可能有300维的空间里，箭头代表的是向量在gender（性别）这一维的差，为了得出类比推理，计算当man对于woman，king对于什么，要做的就是找到单词w来使得

$$e_{\text{man}}-e_{\text{woman}}\approx e_{\text{king}} - e_{w}$$

等式成立，即找到单词w来最大化$e_{w}$与$e_{\text{king}} - e_{\text{man}} + e_{\text{woman}}$的相似度，即

$$Find\ word\ w:argmax\ Sim(e_{w},e_{\text{king}} - e_{\text{man}} + e_{\text{woman}})$$

即把$e_{w}$全部放到等式的一边，另一边是$e_{\text{king}}- e_{\text{man}} + e_{\text{woman}}$。应用相似度函数，通过方程找到一个使得相似度最大的单词，如果结果理想的话会得到单词queen

t-SNE算法所做的就是把这些300维的数据用一种非线性的方式映射到2维平面上，可以得知t-SNE中这种映射很复杂而且很非线性。在大多数情况下，由于t-SNE的非线性映射，不能总是期望使等式成立的关系会像左边那样成一个平行四边形

关于相似函数，比较常用的是余弦相似度，假如在向量$u$和$v$之间定义相似度：

$$Sim(u,v)=\frac{u^Tv}{||u||\cdot ||v||}$$

分子是$u$和$v$的内积。如果$u$和$v$非常相似，那么它们的内积将会很大，把整个式子叫做余弦相似度，是因为该式是$u$和$v$的夹角的余弦值

参考资料： 给定两个向量$u$和$v$，余弦相似度定义如下：

$${CosineSimilarity(u, v)} = \frac {u . v} {||u||_2 ||v||_2} = cos(\theta)$$

$u.v$ 是两个向量的点积（或内积），$||u||_2$是向量$u$的范数（或长度）， $\theta$ 是向量$u$和$v$之间的角度。这种相似性取决于角度在向量$u$和$v$之间。如果向量$u$和$v$非常相似，它们的余弦相似性将接近1; 如果它们不相似，则余弦相似性将取较小的值

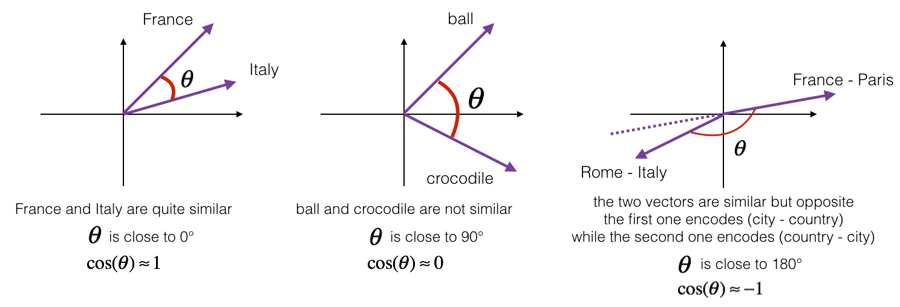
两个向量之间角度的余弦是衡量它们有多相似的指标，角度越小，两个向量越相似

还可以计算Euclidian distance来比较相似性，即$||u-v||^2$。距离越大，相似性越小