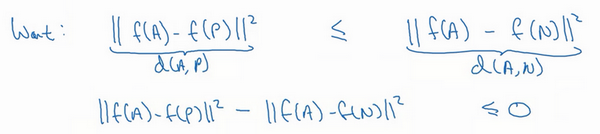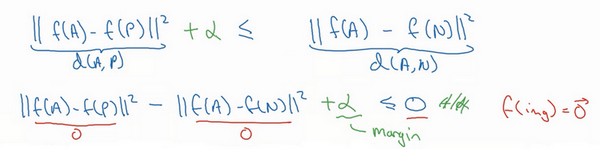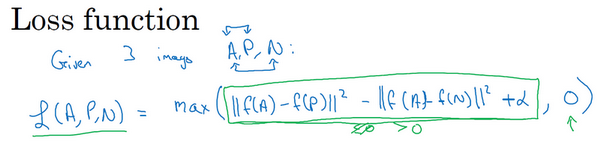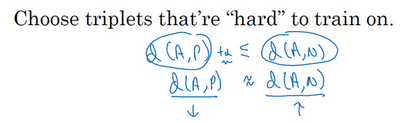4.4 Triplet 损失（Triplet 损失）

要想通过学习神经网络的参数来得到优质的人脸图片编码，方法之一就是定义三元组损失函数然后应用梯度下降

三元组损失每个样本包含三张图片：靶目标（Anchor）、正例（Positive）、反例（Negative），简写成$A$、$P$、$N$

网络的参数或者编码应满足：

让$|| f(A) - f(P) ||^{2}$很小，即：

$$|| f(A) - f(P)||^{2} \leq ||f(A) - f(N)||^{2}$$

$$||f(A)-f(P)||^2-||f(A)-F(N)||^2\leq 0$$

$|| f(A) - f(P) ||^{2}$）是$d(A,P)$，$|| f(A) - f(N) ||^{2}$是$d(A,N)$

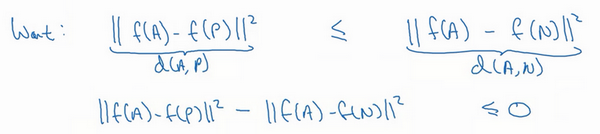
如果所有的图片都是零向量，即$f(A)=0,f(P)=0,f(N)=0$那么上述不等式也满足。但是对进行人脸识别没有任何作用，所以添加一个超参数$\alpha$，且$\alpha>0$，对上述不等式做出如下修改：

$$||f(A)-f(P)||^2-||f(A)-F(N)||^2\leq -\alpha$$

$$||f(A)-f(P)||^2-||f(A)-F(N)||^2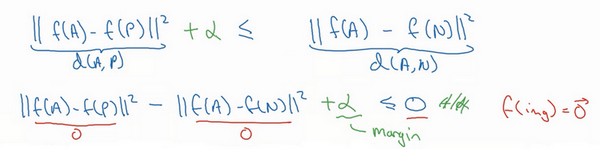+\alpha \leq 0$$

间隔参数$\alpha$也被称为边界margin，类似于支持向量机中的margin，拉大了Anchor和Positive图片对和Anchor与Negative图片对之间的差距。若$d(A,P)=0.5$，$\alpha=0.2$，则$d(A,N)\geq0.7$

损失函数的定义基于三元图片组，即取这个和0的最大值：

$$L( A,P,N) = max(|| f( A) - f( P)||^{2} -|| f( A) - f( N)||^{2} + \alpha,0)$$

$max$函数的作用是只要$|| f( A) - f( P)||^{2} -|| f( A) - f( N)||^{2} + \alpha\leq0$，损失函数就是0

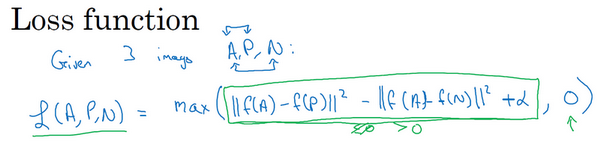
如果$|| f( A) - f( P)||^{2} -|| f( A) - f( N)||^{2} + \alpha\leq0$，最终会得到$|| f(A) - f( P)||^{2} -|| f( A) - f( N)||^{2} +\alpha$，即正的损失值。通过最小化这个损失函数达到的效果就是使这部分$|| f( A) - f( P)||^{2} -||f( A) - f( N)||^{2} +\alpha$成为0，或者小于等于0

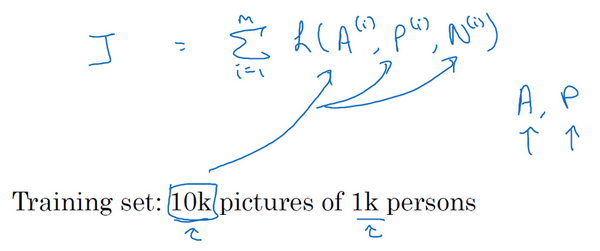
整个网络的代价函数是训练集中单个三元组损失的总和

如何选择三元组来形成训练集：如果从训练集中随机地选择$A$、$P$和$N$，遵守$A$和$P$是同一个人，而$A$和$N$是不同的人这一原则。那么约束条件（$d(A,P) + \alpha \leq d(A,N)$）很容易达到，因为随机选择的图片，$A$和$N$比$A$和$P$差别很大的概率很大，而且差距远大于$\alpha$，这样网络并不能从中学到什么

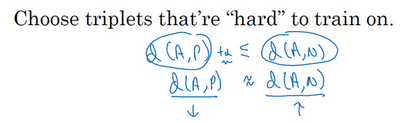
所以为了构建一个数据集，要做的就是尽可能选择难训练的三元组$A$、$P$和$N$：

想要所有的三元组都满足条件（$d(A,P) + a \leq d(A,N)$），$A$、$P$和$N$的选择应使得$d(A,P)$很接近$d(A,N)$，即$d(A,P) \approx d(A,N)$，这样学习算法会竭尽全力使右边式子变大（$d(A,N)$），或者使左边式子（$d(A,P)$）变小，这样左右两边至少有一个$\alpha$的间隔。并且选择这样的三元组还可以增加学习算法的计算效率

总结：

训练三元组损失需要把训练集做成很多三元组，这就是一个三元组（编号1），有一个Anchor图片和Positive图片，这两个（Anchor和Positive）是同一个人，还有一张另一个人的Negative图片。这是另一组（编号2），其中Anchor和Positive图片是同一个人，但是Anchor和Negative不是同一个人，等等。

定义了这些包括$A$、$P$和$N$图片的数据集之后，还需要用梯度下降最小化代价函数$J$，这样做的效果就是反向传播到网络中的所有参数来学习到一种编码，使得如果两个图片是同一个人，那么它们的$d$就会很小，如果两个图片不是同一个人，它们的$d$ 就会很大